Forças de Tração

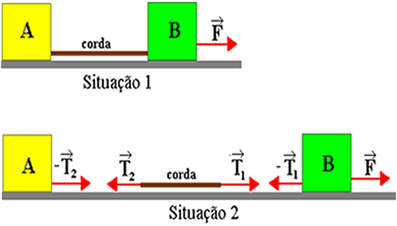
Força exercida em um bloco por meio de uma corda

Força de tração. Determinando a força de tração

Muitas vezes estamos interessados em estudar o movimento não de apenas um corpo, mas de vários corpos, ou seja, às vezes há a necessidade de estudarmos um conjunto de corpos. Denominaremos esses corpos de sistema, seja ele formado por um único corpo, seja ele formado por um conjunto de corpos.

Por exemplo, um astrônomo, num determinado momento, pode estar interessado em estudar apenas o movimento da Terra – nesse caso, o seu sistema é a Terra. Porém, num outro momento, ele pode estar interessado em estudar o movimento conjunto da Terra e da Lua – nesse caso, seu sistema é formado por dois corpos. Em outra situação, ele pode querer estudar o movimento de todo o Sistema Solar pelo espaço – nesse caso, seu sistema possui vários corpos: o Sol, os planetas e os satélites dos planetas.

Forças exercidas por meio de fios

Em determinado momento podemos nos deparar com situações em que forças são exercidas nos corpos, fazendo-se uso de fios. A ilustração acima nos permite ver um exemplo de corpos sujeitos a forças exercidas por meio de fios, onde dois blocos A e B estão ligados por meio de um fio cuja massa vale m_c. Podemos ver que ambos os corpos (blocos) estão sobre uma superfície plana e horizontal sem atrito, sendo puxados por meio de uma força de intensidade .

Na situação 2 da figura acima, representamos as forças atuantes nos blocos e na corda através de diagramas de forças. Podemos ver que a força F está puxando o bloco B, que, por sua vez, puxa a corda exercendo a força T₁. A corda, então, puxa o bloco A, exercendo uma força de intensidade –T₂, e, de acordo com a 3^a Lei de Newton (Ação e reação), o bloco A puxa a corda, exercendo a força T₂.

Não pare agora... Tem mais depois da publicidade ;)

Quando fazemos uso de fios para exercer forças sobre blocos, corpos, sistemas etc., chamamos essa força de Força de Tração. Dessa forma, podemos dizer que T₁ e T₂ são as forças de trações exercidas nas extremidades opostas da corda.

Fazendo uso da 2^a Lei de Newton no fio (corda), obtemos:

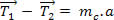
Se observarmos bem a equação acima, podemos ver que as trações 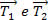 são trações com módulos (valores) diferentes. No entanto, caso a massa da corda seja desprezível, as trações se tornam aproximadamente iguais. Vejamos:

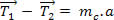(0)

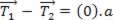
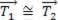
Em geral, usaremos para os respectivos cálculos matemáticos situações em que os fios serão tratados como ideais: ou seja, fios flexíveis, porém inextensível, isto é, que não esticam e possuem massa nula (m = 0).

Pelo que vimos acima, num fio ideal a tração tem a mesma intensidade nos dois extremos do fio.