Lei de Hooke

A Lei de Hooke é usada para calcular o módulo da força elástica que é exercida pelos corpos elásticos de acordo com o tamanho da sua deformação.

 

 

Podemos calcular a força exercida por uma mola esticada ou comprimida a partir da Lei de Hooke.

Ouça: cálculo da força elástica e exercícios resolvidos

Lei de Hooke é a expressão matemática utilizada para calcular a força elástica exercida por um corpo que, quando deformado, tende a voltar ao seu formato original, como molas e elásticos.

Veja também: Aprenda a medir uma força com a Lei de Hooke

A força elástica, determinada pela Lei de Hooke, é uma grandeza vetorial e, por isso, apresenta módulo, direção e sentido. Seu módulo pode ser determinado a partir da equação a seguir:

F – força elástica
k – constante elástica
x – deformação

Essa lei afirma que, quando deformamos um corpo elástico como uma mola, uma força restauradora, chamada de força elástica, surge na mesma direção da compressão feita sobre ela, porém, no sentido oposto. É por esse motivo que há um sinal negativo na fórmula apresentada acima.

Chamamos de constante elástica (k) a propriedade da mola que mede a sua elasticidade. A unidade dessa grandeza é o Newton por metro (N/m). Se uma mola tem constante elástica de 15 N/m, por exemplo, isso indica que é necessário que se aplique sobre ela uma força de 15 N para que o seu tamanho original seja deformado em 1 m. Caso quiséssemos deformá-la, esticando-a ou a comprimindo em 2 m, seriam necessários 30 N.

Já a variável x mede a deformação sofrida por essa mola, ou seja, é uma medida de quanto o seu tamanho foi alterado em relação ao tamanho original. Podemos calcular essa deformação tomando a diferença entre os comprimentos final (L) e original (L_o).

x – deformação (m)
L – comprimento final (m)
L_o – comprimento original (m)

De acordo com o referencial adotado pela Lei de Hooke, caso o valor de x calculado seja negativo (x < 0), isso indica que a mola está sendo comprimida e, nesse caso, oferecerá uma força de resistência positiva (F > 0); no caso contrário, em que a mola é esticada, o módulo da força elástica será negativo (F < 0).

Veja também: Aprenda a resolver exercícios sobre conservação da energia mecânica

Outro fator importante consiste em perceber que, na Lei de Hooke, a força elástica é diretamente proporcional tanto à constante elástica quanto à deformação sofrida pela mola. Isso pode ser percebido facilmente: quanto mais esticamos uma mola, fica mais difícil esticá-la, uma vez que a sua deformação torna-se cada vez maior. Observe o esquema que ilustra essa situação:

Para uma deformação duas vezes maior que a anterior, a força elástica exercida pela mola é duplicada
.

Trabalho da força elástica

É possível calcular o trabalho realizado pela força elástica. Para tanto, usaremos um gráfico simples que relaciona a força elástica com a deformação de uma mola. Observe:

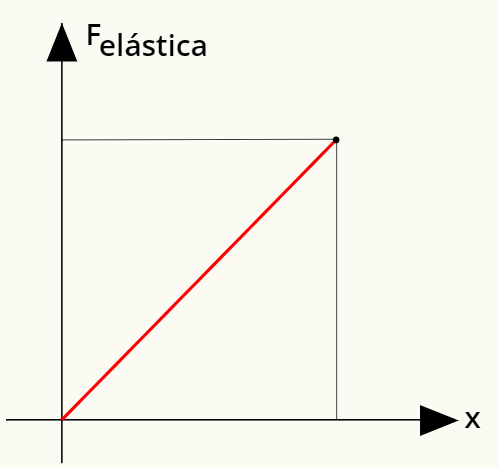
Para calcular o trabalho realizado pela força elástica, basta calcular a área abaixo da reta mostrada no gráfico. Analisando-o, é possível perceber que essa área forma um triângulo, cuja área pode ser determinada a partir do cálculo a seguir:

O resultado acima mede a energia transferida ao se deformar um corpo elástico como uma mola e também equivale àquilo que chamamos de energia potencial elástica.

U_el – energia potencial elástica

Exercícios resolvidos

1) Ao ser esticada do seu tamanho original de 10 cm para 15 cm, uma mola exerce uma força elástica de 50 N. Em relação a essa mola, determine:

a) sua constante elástica em N/m;

b) o módulo de sua energia potencial elástica em J.

Resolução

a) Podemos calcular a constante elástica dessa mola usando a Lei de Hooke. Para tanto, devemos observar que a deformação x deve ser dada em metros. Observe:

b) Para determinarmos o módulo da energia potencial elástica armazenada nessa mola, basta fazermos o cálculo a seguir: